표본평균이 모평균이랑 같은 게 아니라
표본평균의 평균이 모평균과 같은 것!
어떤 집단에 대해 통계 분석을 진행한다고 가정해보자. 이때 해당 집단의 전체 구성원이 그리 많지 않다면 전수 조사를 진행할 수 있다. 전수 조사가 가능하다면 기술통계적으로 접근해 각종 통계량을 쉽게 도출해낼 수 있다. 그러나, 대한민국 전국민 5000만 명을 대상으로 통계조사를 진행한다고 가정한다면 얘기가 달라진다. 5000만 명을 일일이 전수 조사하는 것은 사실상 불가능에 가까울 뿐더러, 설사 감행한다고 하더라도 막대한 비용을 감수해야만 한다.(과거 인구주택총조사를 전수조사로 진행한 적은 있지만, 전국민을 대상으로 한 전수조사는 매우 이례적인 경우다)
이처럼 대한민국 전국민을 통계 조사를 통해 알고 싶은 '대상'이라고 가정했을 때, 대한민국 전국민을 population(모집단)이라고 한다. 그리고 5000만 명을 대상으로 일일이 전수조사하는 것은 시간적으로나 비용적으로나 소모가 크기 때문에 5000만 명 중 여러 표본들을 추출해 결과적으로 전국민의 10%인 500만 명을 샘플링한다. 추출한 500만 명을 표본집단이라고 하고, 이 표본을 통해 모집단의 특성을 '추정'하는 것을 추론 통계(Inferential Statistics)라고 한다.
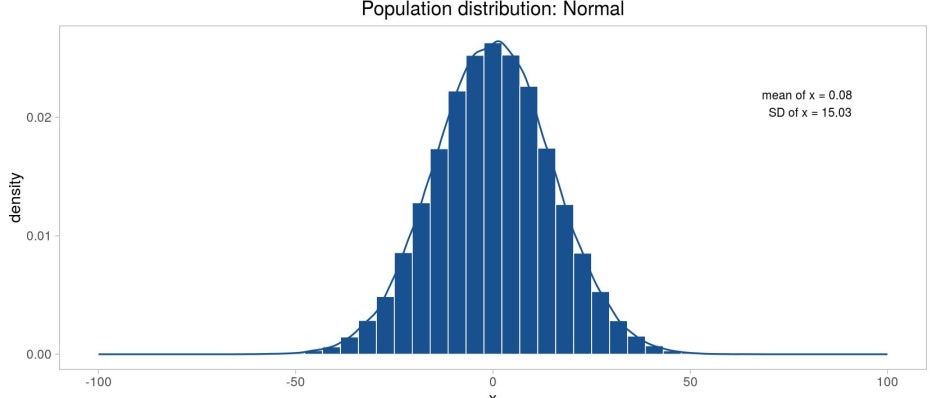
이렇게 표본을 추출할 때 편향을 최소화하기 위해 임의 추출(무작위 추출, random sampling)과 복원 추출을 전제하고 진행한다. 위의 그림을 정규분포를 따르는 전국민 5000만 명의 분포라고 가정해보자. 그리고 아래는 500만 명의 표본을 추출하기 위해 추출한 샘플들이다.
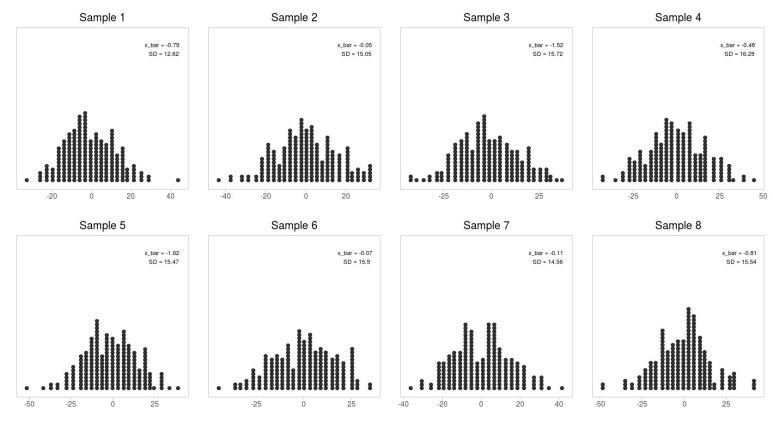
이 때, 표본 500만 명의 평균과 분산을 각각 '표본평균(Sample mean, 엑스바)'과 '표본분산(Sample variance, S)'라고 한다. 보통 표본평균의 개념을 '고정된 값'으로 오해하는 경우가 많은데 표본평균은 절대 고정된 값이 아니다. 표본을 추출할 땐 임의로, 그리고 반복적으로 추출하는데 당연히 추출할 때마다 표본이 달라진다. 매번 추출할 때마다 표본이 달라지므로 표본평균 역시 달라지는 것은 당연하다. 위의 Sample 분포를 보면 알 수 있듯이, 각 샘플마다 표본평균 엑스바의 값이 상이하다. 표본분산 역시 마찬가지다.
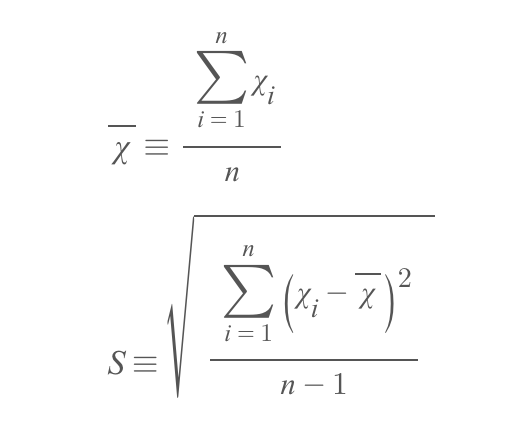
표본표준편차에서 분모가 n이 아닌 n-1인 이유는 불편분산 개념 때문인데 불편분산에 대해선 이후의 포스팅에서 다룰 예정)
위의 그림에서 각 샘플마다 표본평균의 값이 다르다는 것은 이제 알 것이다. 그러면, 이 표본평균들로부터 표본평균의 평균과 분산을 도출할 수 있다.
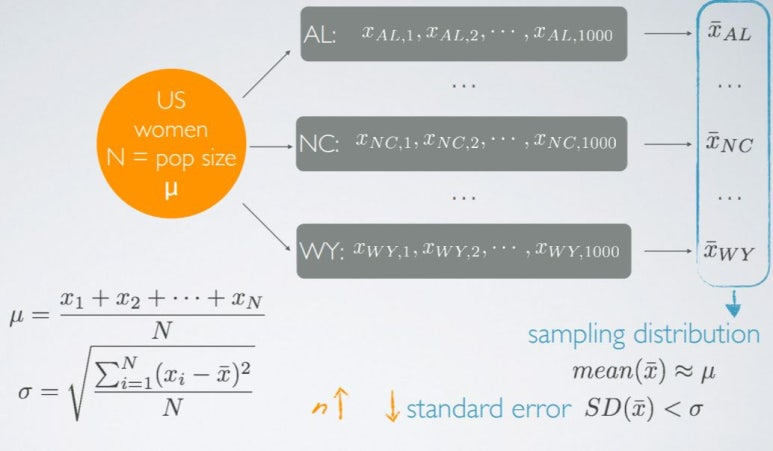
예를 들어, 미국 여성들의 평균 신장을 구하려고 한다. 이를 위해 각 주(state)마다 1000명의 표본을 추출했다. 워싱턴, 뉴욕 등 50개의 주에서 추출한 샘플들로부터 각각 구한 평균값이 표본평균이다. 이 표본평균은 각 주마다 다르다. 워싱턴의 표본평균은 161일 수 있고, 뉴욕에서의 표본평균은 155일 수 있다. 이런 이유로 아까 위에서 표본평균은 고정된 값이 아니라고 한 것이다. 표본평균은 샘플링을 할 때마다 다른 값이 나오므로 당연히 모평균(mean of population)과 같을 수 없다.
표본평균들을 새로운 확률변수로 생각하고 이 값들의 평균을 구할 수 있는데, 이를 '표본평균의 평균(표본평균의 기댓값)'이라고 하며 이 값이 모평균과 같다.
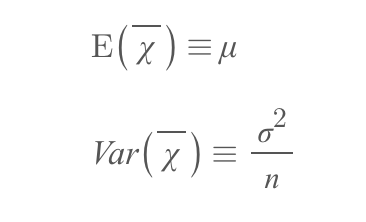
여기에서 또 하나의 개념을 도출할 수 있는데 바로 '표준오차(Standard Error, SE)'다.

Central Limit Theorom
중심극한정리
이처럼 현실에서 통계 분석을 하기 위해선 모집단으로부터 표본을 추출하고 그 표본들의 통계량을 통해 모집단을 추정한다. 그런데, 통계학을 공부하다보면 표본의 크기(size), 즉 n이 충분히 크면 대표성을 띤다는 말을 자주 듣게 되는데 이를 이해하기 위해선 '중심극한정리(Central Limit Theorom)'을 알아야 한다.
중심극한정리는 한 마디로, '동일한 확률 분포를 지닌 확률변수 n개의 평균의 분포는 n이 충분히 클 때 정규분포에 가까워진다'라는 개념인데 즉, 표본이 클수록 표본평균의 분포가 정규분포 모양에 가까워진다는 의미다. 여기서 주의해야할 점은 표본들의 분포가 아니라 '표본평균들이 이루는 분포'가 정규분포에 가까워진다는 것.
또, 하나 특이한 점은 모집단이 어떤 분포의 모양이든간에(균등분포이든 왜도이든 정규분포이든) 표본이 많아질수록 표본평균의 분포는 정규분포의 형태를 띤다는 것이다. 이 중심극한정리가 중요한 이유는 추론통계학을 떠받치고 있는 기둥 중 하나이기 때문이다. 무엇보다도 중심극한정리를 통해 표본평균들의 분포와 모집단 간의 관계를 증명할 수 있다. 모집단이 어떤 분포이든, 그리고 충분히 많은 표본을 추출했다면 그 표본들의 평균 '표본평균'의 분포는 정규분포에 근사하고, 이를 통해 Z값을 활용할 수 있다. 즉, 추출한 표본의 통계량으로 모집단의 특징들, 모수를 설명할 수 있는(추정할 수 있는) 수학적인 근거를 제공하는 셈이다.
CLT for means
gallery.shinyapps.io
위의 링크는 모집단의 분포, 평균, 표준편차, 샘플 크기, 샘플 개수 등을 사용자 임의로 설정하고 그 결과로 분포 모양이 어떻게 변화하는지를 시뮬레이션으로 확인해볼 수 있는 사이트다. 링크 들어가서 시뮬레이션을 해보면 왼쪽으로 심하게 치우친 왜도(Right-skewed distribution)의 샘플 크기를 늘림으로써 표본평균의 분포가 정규분포 모양으로 변하는 것을 확인할 수 있다.
'Product Analytics > Statistics' 카테고리의 다른 글
| [Stat] 베이즈 정리를 위한 전확률 공식(formula of total probability) (3) | 2024.12.24 |
|---|---|
| [Stat] 추측 통계학의 꽃 '가설 검정'(귀무가설, 대립가설) (4) | 2024.12.24 |
| [Stat] 회귀모형 평가하기 - RMSE(평균 제곱근 오차) (2) | 2024.12.24 |
| [Stat] 선형회귀(linear regression), 최소제곱법 (0) | 2024.12.24 |