[Stat] 베이즈 정리를 위한 전확률 공식(formula of total probability)
베이즈 정리
확률론과 통계학에서, 베이즈 정리(영어: Bayes’ theorem)는 두 확률 변수의 사전 확률과 사후 확률 사이의 관계를 나타내는 정리다. 베이즈 확률론 해석에 따르면 베이즈 정리는 사전확률로부터 사후확률을 구할 수 있다.
베이즈 정리는 불확실성 하에서 의사결정문제를 수학적으로 다룰 때 중요하게 이용된다. 특히, 정보와 같이 눈에 보이지 않는 무형자산이 지닌 가치를 계산할 때 유용하게 사용된다. 전통적인 확률이 연역적 추론에 기반을 두고 있다면 베이즈 정리는 확률임에도 귀납적, 경험적인 추론을 사용한다. (출처: https://ko.wikipedia.org/wiki/%EB%B2%A0%EC%9D%B4%EC%A6%88_%EC%A0%95%EB%A6%AC)
통계학에서 확률을 다룰 때 크게 두 가지의 관점이 존재한다. 빈도주의(Frequentism)와 베이즈주의(Bayesianusn)가 바로 그것인데, 이 두 관점은 서로 갈등을 빚기도 했다. 빈도주의자들은 베이즈주의를, 베이즈주의자들은 빈도주의를 비판하며 갈등 구도를 형성하기도 했다. 개인적으로는 베이즈 통계의 논리가 좀 더 설득력있다고 생각하는 편이지만, 빈도주의적 관점 역시 유용하게 쓰인다고 생각한다. 베이즈 정리는 잘못된 정보(noise)를 걸러내거나 기상, 지진, 전염병 확산 예측 등 다양한 목적으로 활용된다.
3번의 포스팅(전확률 공식, 조건부 확률, 베이즈 정리)에 걸쳐서 베이즈 정리를 통계적으로 다뤄볼 예정이며 그 과정에서 사용되는 개념과 공식을 독립적으로 제시하기보다는 각 개념이 어떻게 이어지고, 각 공식이 어떻게 연결되는지를 '이해하는 관점'에서 서술해보려 한다. 별로 좋아하는 표현은 아니지만 통계를 문과식으로 이해해보자는 시도이다.
베이즈 정리를 이해하기 위해선 다양한 개념들을 먼저 이해해야 한다. 베이즈 정리를 위해선 조건부 확률(conditional probability)과 전확률 공식(formula of total probability)을 이해해야 하는데 각 개념의 공식을 단순히 암기하기 보다는 도출되는 과정을 이해하는 게 좋다. 베이즈 정리에 대한 자세한 설명 이전에 전확률 공식을 먼저 이해해보자.
표본공간
전확률 공식을 이해하기 전에 우선 표본공간의 분할에 대해 알아야 한다. 우선, 표본공간(sample space)이란 어떠한 목적 하에 실험을 하였을 때 관찰할 수 있는 모든 결과의 집합을 의미한다. 예를 들어, 1부터 6까지 적혀있는 정육면체 주사위를 한 번 던진다면 표본공간 S는 아래와 같이 된다.
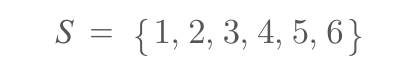
여기서 주사위의 눈이 3과 5가 나오는 경우를 '사건(event)'라고 하며, 주사위 눈이 3과 5가 나오는 사건은 표본공간 S의 부분집합이라고 볼 수 있다.
고전적 확률, 공리론적 확률
고등교육을 통해 확률(probability)의 의미에 대해선 대부분이 직관적으로 이해하는 편이다. 그러나, 통계학을 제대로 이해하기 위해선 근간이 되는 확률의 의미를 정확하게 수리적으로 파악하는 것이 중요하다.
우선, 확률에는 크게 고전적 확률(classical probability)과 공리론적 확률(axiomatic probability)이 있다.
위의 예와 마찬가지로 1부터 6까지 적혀있는 정육면체의 '공정한' 주사위가 있다고 해보자. (6이 많이 나오게끔 특수 제작된 주사위의 경우엔 '공정하지 않은' 주사위인 셈이다) 이런 공정한 주사위가 있다고 가정했을 때 주사위 눈이 3인 사건(부분집합)이 나올 확률을 우리는 자연스럽게 1/6이라고 알고 있다. 그러나, 만약 주사위를 10번만 던진다면 즉, 유한한 횟수 동안만 주사위를 던진다면 주사위 눈이 3인 사건일 확률은 1/6이 아닐 가능성이 높다. 10번 중 10번 모두 1만 나올 수도 있고, 1번만 3이 나올 수도 있기 때문이다.

그러나, 이 주사위를 무한하게 반복해서 던진다면 주사위 눈이 3인 사건이 나올 확률은 1/6에 가까워진다. 즉, 우리가 일반적으로 주사위의 각 눈이 나올 확률을 1/6으로 생각하는 사고 과정은 주사위를 한 번 던졌을 때 나올 수 있는 모든 경우로 구성된 표본공간 {1, 2, 3, 4, 5, 6}에 대해 3이 나오는 사건 A={3}의 상대적인 비율을 자연스레 고려한 결과이다. 즉, 고전적 확률은 유한개의 원소로 구성된 표본공간에 존재하는 원소들이 거의 동등하게 나타나는 경우에 사용되며, 위와 같이 어떠한 부분집합, 즉 어떤 사건 A가 나타날 확률은 표본공간 내의 원소 수에 대한 사건 A에 포함된 원소 수의 상대적 비율이다.

원소 수가 유한한 표본공간에서 사용하는 고전적 확률과 달리 공리론적 확률은 표본공간 내의 원소 수를 셀 수 없을 때 사용한다. 예를 들어, 원판에 다트를 던진다고 가정해보자. 표본공간은 원판 위의 눈으로 확인할 수 없는 수많은 점이며, 중앙의 빨간 영역에 다트가 꽂히는 사건 A의 확률을 구하고 싶다고 해보자. 주사위를 던지는 실험과는 달리 다트를 던지는 실험에서는 표본공간의 원소가 유한 개가 아니다. 즉, 원판의 셀 수 없을 정도로 많은 점의 개수(표본공간)에 대해 중앙에 다트를 꽂는 사건 A에 포함된 원소 수의 상대적인 비율을 구할 수 없다. 결국, 고전적 확률로는 가능성을 도출할 수 없는 것이다.
그래서 사용되는 것이 콜모고로프(Kolmogorov)의 공리론적인 확률이다.
공리론적 확률은 세 가지의 공리(콜모고로프 공리)를 지켜야만 한다.
공리 (1) 모든 사건에 대해 확률은 실수이고 0 또는 양수이다.

공리 (2) 표본공간(전체집합)이라는 사건(부분집합)에 대한 확률은 1이다.
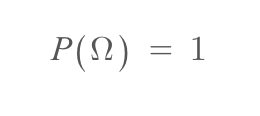
공리 (3) 공통 원소가 없는 두 사건의 합집합의 확률은 사건별 확률의 합이다.

공리 3은 A와 B가 서로 배반사건이면 두 사건의 합집합의 확률은 각 사건의 확률을 더한 것과 같다는 의미이다. 콜모고로프 공리를 지킨다는 가정 하에 공리론적 확률의 개념은 다음과 같다. 기하학적 의미의 확률이라고 보면 된다.

표본공간의 분할
더 나아가 전확률 공식에서 유용하게 사용될 표본공간의 분할(partition)에 대해 알아보자.
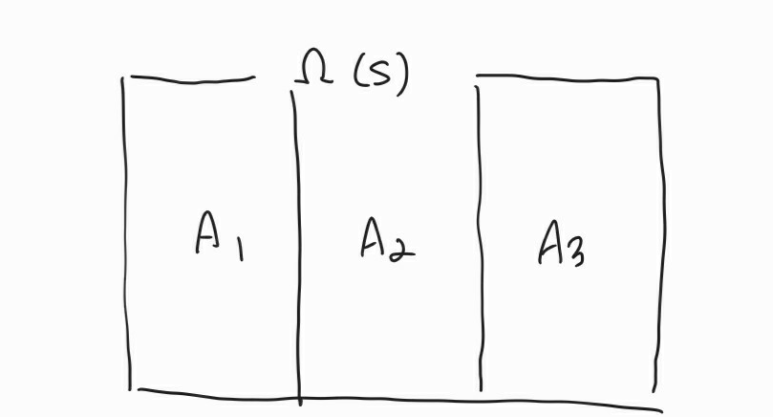
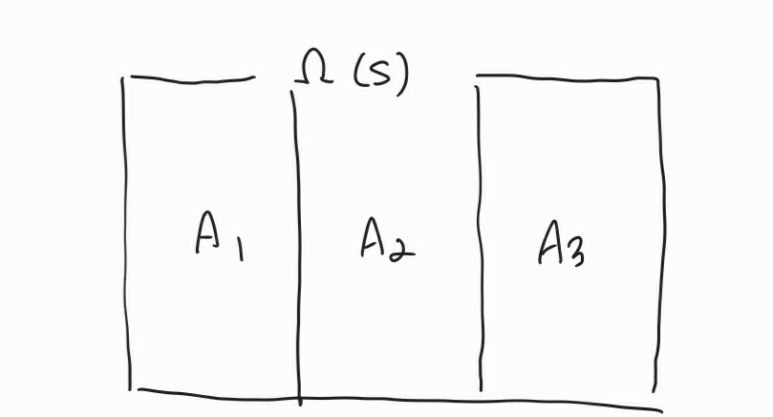
우선, 표본공간에 3개의 사건 A1, A2, A3이 존재한다. 이때 아래의 두 가지 조건을 만족하는 사건들을 표본공간의 분할이라고 한다.
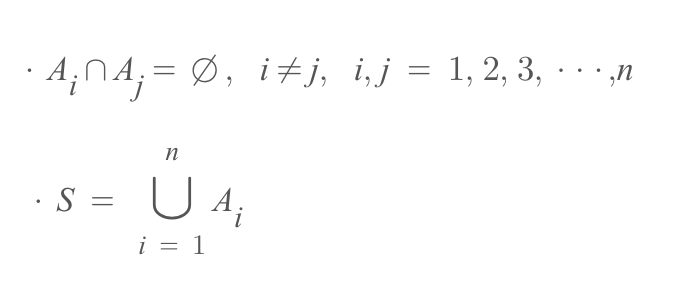
전확률 공식(전체확률 공식)
전확률 공식(전체확률 공식)은 이후에 나올 베이즈 정리를 이해하는 데에 중요한 개념이다. 전확률 공식은 베이즈 정리에서 정규화 상수(normalizing constant) 혹은 증거(evidence)를 의미하는 P(B)를 구하는 데에 사용된다.
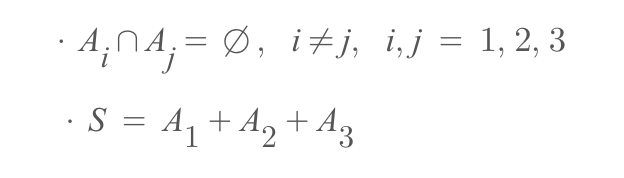
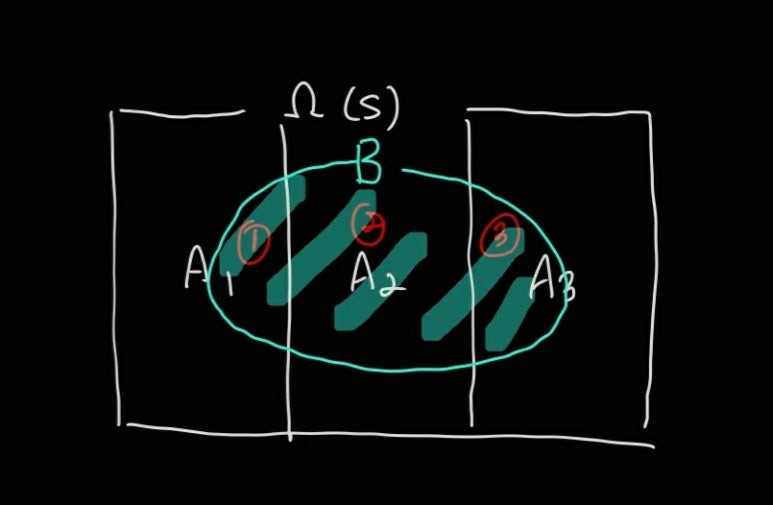

사건 B의 확률과 Ai(i=1, 2, 3) 사건들의 각 확률의 교집합의 합이 결국 사건 B의 확률이 된다. 이를 각각 ①, ②, ③로 표시하였으며 각각은 B와 A1의 교집합, B와 A2의 교집합, B와 A3의 교집합으로 표현할 수 있다. 그 다음, 각 교집합 확률을 빨간 박스처럼 조건부확률로 표현할 수 있다. 조건부확률과 결합확률에 대한 자세한 설명은 다음 포스팅에서 할 예정이기 때문에 우선은 간단하게 교집합이 저렇게 표현되는 과정만 제시하겠다.

A와 B의 교집합 확률은 간단하게 P(A, B)로 표현하기도 한다. 두 사건의 교집합을 조건부확률을 활용해 표현하면 위와 같이 되는데 이를 좀 더 이해하기 쉽게 설명하자면 다음과 같다.
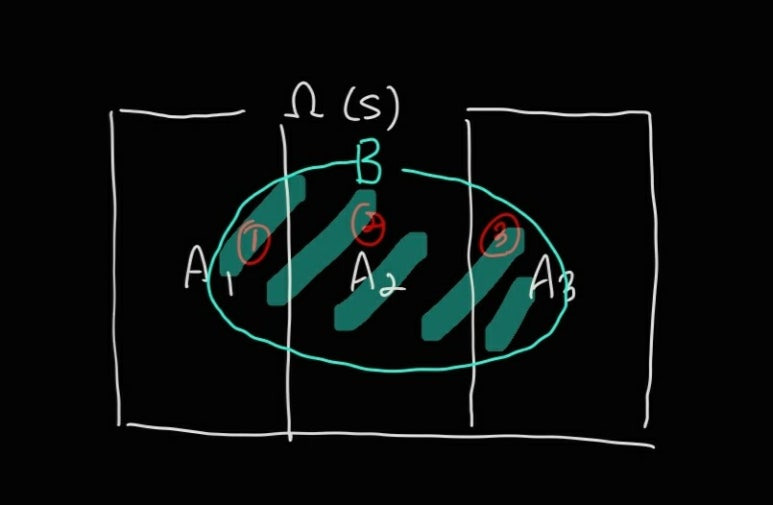
위에서 말했듯이 B 사건의 확률은 A1과 B의 교집합 확률, A2와 B의 교집합 확률, A3와 B의 교집합 확률의 합이다. 그리고 각 교집합 확률은 조건부확률의 정의에 따라 조건부확률을 활용해 표현할 수 있다. 공식으로 도출하는 것이 아니라 논리적으로 생각해보면 표본공간에서 A1과 A2, A3이라는 사건이 존재하고, 이 상태에서 표본공간 내에 B라는 임의의 사건이 발생했다. 즉, 위 그림에서 ①은 우선 A1사건이 발생해야 하고, 그 다음에 A1이는 새로운 표본공간에서 B라는 사건이 발생한 것이다. 다시 말해, (1) A1사건이 발생하고 (2) A1이라는 표본공간에서 B라는 사건이 발생할 확률이 결국 A1과 B의 교집합 확률인 것이다.

이를 활용해 사건 B의 확률을 구할 수 있다.